A partire dall’osservazione del mondo naturale e ispirandoci in particolare alla capacità costruttiva delle api, abbiamo sperimentato la costruzione di un prototipo di cupola geodetica, realizzata a scopo didattico e dimostrativo.
GEOMETRIE NATURALI E ARCHITETTURA
Da sempre l’uomo guarda alla natura e alle sue forme, le studia per comprendere il modo attraverso cui si costituiscono e ne trae ispirazione per creare, a sua volta, le proprie opere. Lo scienziato Galileo Galilei, già nel XVII secolo, ha individuato nella geometria il linguaggio indispensabile per poter comprendere la natura.
Pensiamo al mondo naturale e alle sue geometrie: alcune sono immediatamente riconoscibili, altre non sono visibili a occhio nudo. Ad esempio, il capside dei virus (la struttura che ne contiene il DNA) può avere la forma di un icosaedro; la forma delle molecole di alcuni cristalli e minerali è talvolta assimilabile a quella di solidi regolari: nel caso del cloruro di sodio, il comune sale da cucina, gli atomi si dispongono in cubi; nella grafite, utilizzata per realizzare matite, gli atomi formano strati composti da esagoni; nei fullereni gli atomi di carbonio generano maglie composte da esagoni e pentagoni. Sono poi molti i cristalli che si strutturano seguendo le composizioni e le varianti dei solidi regolari, cioè di quei solidi che impareremo a chiamare “solidi platonici”.

Geometrie naturali © AR CO
Se consideriamo lo studio delle forme operato dall’uomo, ci accorgiamo come in esso l’interesse si concentri sull’aspetto geometrico; ne costituiscono esempio i poliedri regolari di Platone, le decorazioni delle architetture arabe come quelle che si possono ammirare all’Alhambra di Granada, l’opera di M. C. Escher e le sue “Metamorfosi”, e ancora le grandi coperture degli architetti contemporanei.

Mosaico Alhambra, Escher "Metamorfosi", fiera di Milano © AR CO
DAL MONDO DELLE API ALLA TASSELLAZIONE GEOMETRICA
La matrice esagonale degli alveari costruiti dalle api è forse il caso più noto di geometria naturale ed è dal suo studio geometrico che vogliamo partire.

Matrice esagonale degli alveari © AR CO
Il problema per le api è quello di costruire nel modo più efficiente possibile una struttura piana suddivisa in aree uguali, senza lasciare vuoti né incorrere in sovrapposizioni; questo problema in geometria si chiama tassellazione del piano.
Non tutte le figure sono in grado di tassellare il piano e il modo più semplice è quello di usare i poligoni regolari, quelle figure piane che hanno lati e angoli tutti uguali. Prendiamone in considerazione alcuni: il triangolo equilatero, il quadrato, il pentagono, l’esagono e l’ottagono. È facile sperimentare, per esempio con dei ritagli di carta, come di questi poligoni solo il triangolo equilatero, il quadrato e l’esagono siano in grado di tassellare il piano. Ma di questi tre poligoni qual è il più efficiente dal punto di vista applicativo? Quale necessita della minor quantità di materiale, tempo e lavoro per essere realizzato? Queste domande dal punto di vista geometrico devono essere formulate in questo modo: a parità di area, quale dei tre poligoni ha il perimetro più breve?
Con dei semplici calcoli si dimostra che l’esagono è il poligono che racchiude la superficie data nel perimetro più breve e dunque è la figura che stavamo cercando. La natura ha insegnato alle api che l’esagono è la scelta giusta per costruire i favi e loro applicano questa regola spinte dall’istinto.
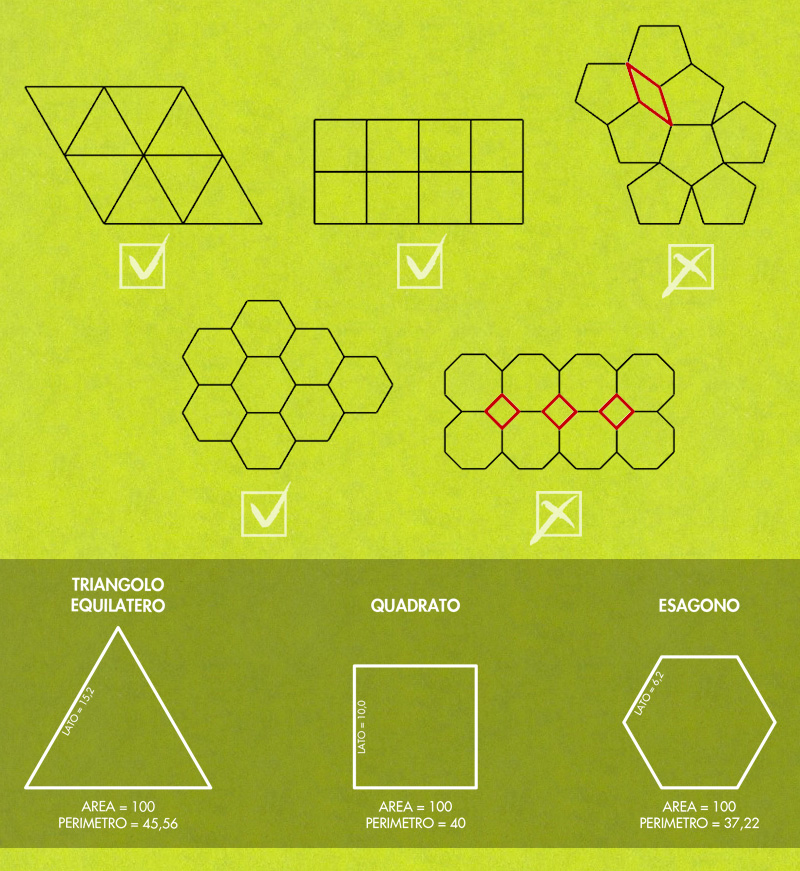
Poligoni e tassellazione del piano © AR CO
Il problema della tassellazione può essere esteso dal piano alle superfici curve, fino allo spazio. I modi per realizzare una tassellazione tridimensionale sono più complessi perché fanno riferimento a figure solide che generalmente sono meno note rispetto ai poligoni piani che abbiamo appena visto. Ne esistono comunque molti, il più semplice dei quali fa riferimento ai solidi regolari. Essi sono solo 5: il tetraedro, l’esaedro o cubo, l’ottaedro, il dodecaedro e l’icosaedro. Di questi unicamente il cubo è in grado di formare una struttura capace di tassellare lo spazio senza lasciare vuoti o intersecarsi.
Le proprietà di questi solidi li rendono tanto particolari da essere stati studiati già nell’antichità greca. In particolar modo fu Platone, da qui il loro nome di “solidi platonici”, a dar loro un fondamentale ruolo nella descrizione del cosmo, assegnando ad ognuno uno degli elementi naturali: il fuoco corrisponde al tetraedro, la terra al cubo, l’aria all’ottaedro, l’acqua all’icosaedro e il cosmo tutto al dodecaedro.
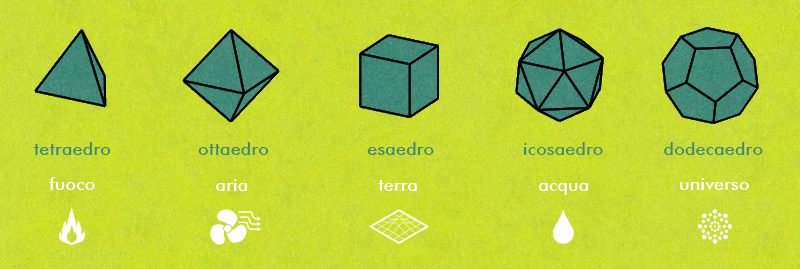
I solidi platonici e la loro associazione con gli elementi naturali © AR CO
LA CUPOLA GEODETICA
Uno dei solidi platonici, l’icosaedro, è anche la matrice geometrica di partenza per poter realizzare la tassellazione di una superficie curva come la sfera. La struttura geometrica che si viene a realizzare viene detta geodetica (termine coniato dall’architetto americano Buckminster Fuller). Il procedimento prevede che si inscriva un icosaedro all’interno della sfera da tassellare (a) e che si proiettino, dal centro della sfera sulla sua superficie, i vertici e i punti medi degli spigoli dell’icosaedro (b). L’insieme dei punti così individuati sulla sfera può essere collegato attraverso una rete di segmenti che costituisce la struttura geodetica propriamente detta (c). Il numero di vertici della geodetica dipende dal numero di parti in cui vengono divisi gli spigoli dell’icosaedro inscritto prima di essere proiettati sulla sfera.
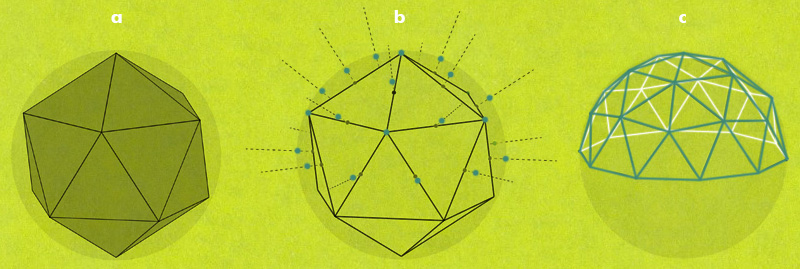
Dall'icosaedro alla cupola geodetica © AR CO
La struttura della geodetica è una delle più efficaci dal punto di vista costruttivo: consente la copertura di superfici a terra molto estese, utilizzando elementi modulari di dimensioni notevolmente ridotte rispetto a quelli di un più tradizionale schema costruttivo. Osservandola possiamo notare alcune caratteristiche geometriche che contribuiscono alla sua efficacia statica: la struttura è suddivisa in triangoli che possono alternativamente essere raggruppati in pentagoni o esagoni; inoltre è caratterizzata da una spiccata simmetria in tutte le direzioni.
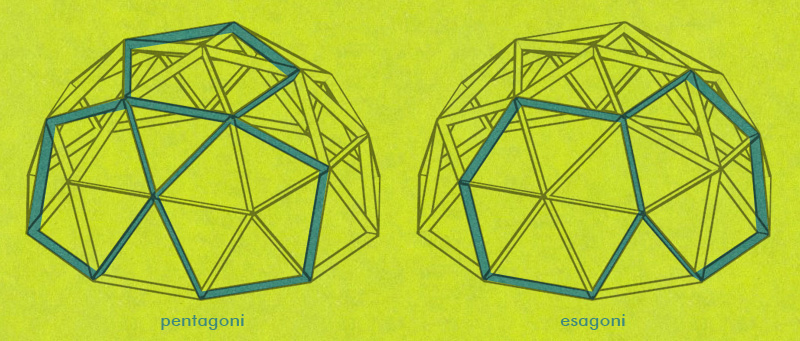
La cupola geodetica © AR CO
I moduli triangolari a differenza di qualsiasi altra figura piana, sono indeformabili, non possono cioè assumere altre configurazioni anche se sottoposti a forze esterne.
La simmetria della geodetica e l’elevato numero di nodi ed elementi che la costituiscono garantiscono una efficace e regolare distribuzione dei carichi applicati alla struttura. Possiamo visualizzare questi carichi come dell’acqua che scorre lungo le aste che la compongono: se versiamo l’acqua sul vertice più alto della geodetica questa si dividerà in tante porzioni quante sono le aste che convergono su quel vertice; ancora, immaginiamo di seguire il percorso di due porzioni di acqua che scorrono lungo due aste contigue, queste finiranno per incontrarsi di nuovo in un vertice della struttura ma, dato che sono quantità uguali e che arrivano secondo due direzioni simmetriche e opposte, parte della forza viene dissipata.









